Skip to main content

Minterm and maxterm in Digital logic design - Computer Science fundamentals tutorial


Minterm and Maxterm
First thing to know before we proceed  towards  what is ‘minterm’ and ‘maxterm’ we have to know the sum of product and product of sum.

Sum of product: - The logical sum of two or more logical product term is called sum of products expression. It is basically an OR operation of AND operated variables such as
Y = AB+BC+ABC

Product of Sum: - The logical product of two or more logical sum term is called product of sums expressions. It is basically an AND operation of OR operated variables such as
Y = (A+B).(B+C).(A+B+C)

Minterm: -Product term containing all the k variables of the functions is either complimented or uncomplimented form is Minterm.


Canonical form of sum of product: - It is defined as the logical sum of all the minterms derived from the rows of a truth table for which value of the function is 1. It is called a minterm canonical form. The canonical sum of product expression can be given in a compact form by listing the decimal code in correspondence with the minterm containing the function value 1.
                   If any sums of products expressions are not in canonical form then we can use the following procedure to obtain canonical sum of products.
   1. Examine each term in given logic function retain it. If it is a minterm continue to examine the term in the same manner.
   2.   Check for variables that are missing each product which is not a minterm. Multiply product by (X+=1) for each variable X that is missing.
   3.   Multiply all the products omit redounded terms.
Example of Minterm
Obtain the canonical sum of product from of the function


Maxterm: -
A sum term containing all the k variable of the function in either complimented or uncomplimented form is called maxterm. Each maxterm can obtain by OR operation of all the variables of the function in a maxterm variable appears either in uncomplimented form if it possess the value 0 in corresponding combination or complimented form if it possess the value of 1

Canonical form of Canonical form of sum of product: -
This is defined as the logical product of all the maxterm derived from the rows of truth table for which the value of function is ‘0’. It is also known as maxterm canonical form. The canonical product of sum expression can be given in a form by listing decimal code corresponding to the maxterm containing function value of ‘0’. If any product of sum expression are not in canonical form of product of sum expression by using following procedure:-
1.Examine each term in the given logical function retain it. If its maxterm continue to examine the next term in the same manner.
     2.  Check for variables that are missing in each sum which is not a maxterm.ADD(X.=0) to the sum term for each variable X that is missing.
     3. Expand the expression using the distribute property and eliminate the redounded term.
Example of maxterm: -


Labels:

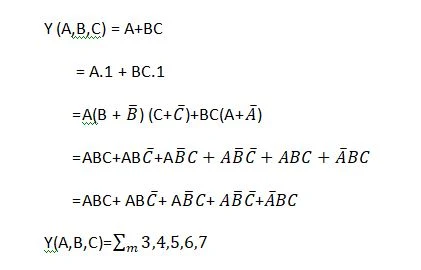
Comments

Post a Comment

please subscribe my blog and let me suggest how I improve this site

Popular posts from this blog

type casting in C. - computer science fundamentals tutorial

Typecasting in C Typecasting is also known as "forced conversion". It refers to changing variable one data type to another data type.          Typecasting in can be certified into following two types: - 1) Implicit type casting. 2) Explicit type casting. Implicit type casting : - It is also known as "Automatic type conversion". It is done by compiler on its own without any external trigger from user. Generally takes place when in an expression more than one data type is present in such condition. Type conversion take places to avoid data lose. Example : - #include<stdio.h> main() {   char y = 'a';   int b = y; printf("%c",y); printf("%d",b); } Explicit Type casting : - This process also called 'Type casting' and it is user defined . Here the user can type cast the result to make it of particular data type. Example : - #include<stdio.h> main() { int m...
2 comments
Read more

Important MCQ of RDBMS( Relational database management system)-FCST

Important MCQ of RDBMS  1. A RDBMS consists a collection of ? a. Tables b. Fields c. Records d. Keys  ANS/- a. table 2. The term attribute refers to a ___________ of a table a. Record b. Tuple c. Column d. Key   ans/- c. Column 3. In relational model, the row of table is known to be ?  a. Relation b. Entity field c. Tuple d. Attribute  ans/- C. Tuple 4. . Address field of a person should not be part of primary key, since it is likely to ? a. Dependent b. Too long c. Changed d. Not changed  ans/- c. Changed 5. The relational model is concerned with ? a. Data structure and Data integrity b. Data Manipulation c. Both a and b d. None of these  ans/- c. Both a and b 6. Which is the false statement from the following ? a. A veiw is a named derived table b. A name relation is variable c. A veiw is a named reation and is virtual d. None of these  ans/- d. None of these 7. The union of primary key...
6 comments
Read more

Solve-write C program to find grade of student by using nested else-if statement

C program to find grade of student by using nested else-if statement Problem Description This program take input as your number then show your grade. Problem Solution 1. enter your marks as input. 2. then check your marks with 'If' block's condition. if it satisfied then show your grade as output. 3. if it not satisfied then it checks with all else-if block's condition repeatedly. 4. print the grade according to your given marks as input and exit. Program codes:-   #include<stdio.h> main() { int n; printf("\n enter the marks:"); scanf("%d",&n); if(n>89) printf("O"); else if(n>79) printf("E"); else if(n>69) printf("A"); else if(n>59) printf("B"); else if(n>49) printf("C"); else if(n>39) printf("D"); else printf("F"); } Program explanation:- 1. enter your marks. for example we take 70 . ...
Post a Comment
Read more